【Unity】列挙型にビット演算を用いて同時にフラグをたてれるようにする

はじめに

今回は列挙型にビット演算を用いて同時にフラグをたてれるようにする記事になります！

突然ですが、こちらのコードを見てみてください。

public enum Magic
{
    Hyado,
    Gira,
    Hoimi,
    Mera
}

いわゆる列挙型といういうやつですね。ドラクエの魔法を列挙型で表現してみました。

ただこの魔法を複数習得したいときってないでしょうか？いまの状態だと4つのうち一つしか習得できません。

そんなときはビット演算を用いることで簡単に表現することができます。

ということで早速みていきましょう！

ビットフラグとは

まずはビットフラグという考え方についてみてみましょう。この画像をみてみてください。

f:id:hanaaaaaachiru:20191005184426p:plain

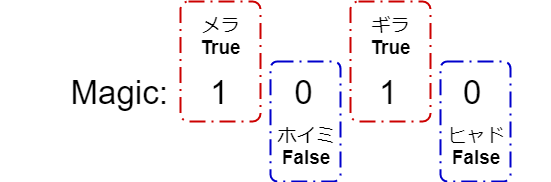
これはMagicはint型の10という数字ですが、2進数で表すと1010になります。

その1010に先頭からbool型のメラ・ホイミ・ギラ・ヒャドを対応させているイメージです。

数字が1ならTrue，0ならFalseという訳ですね。

列挙型を定義する

先程のビットフラグを列挙型にも用いてみましょう。以下のようなコードを書いてみます。

public enum Magics
{
    Hyado = 1 << 0,     //2進数だと0001　(10進数だと1)
    Gira = 1 << 1,      //2進数だと0010　(10進数だと2)
    Hoimi = 1 << 2,     //2進数だと0100　(10進数だと4)
    Mera = 1 << 3       //2進数だと1000　(10進数だと8)
}

これで先程のビットフラグの例と対応した列挙型が作成できました。

<<はビットシフトというもので、1 << 2という操作をすると0001(10進数で1)が0100(10進数で4)という感じで左に2個ずらすことができます。

ちなみにこのように書いてもＯＫです。

public enum Magics
{
    Hyado = 1     //2進数だと0001
    Gira = 2,      //2進数だと0010
    Hoimi = 4,     //2進数だと0100
    Mera = 8       //2進数だと1000
}

最後にFlags属性をつけてあげることで完成です。ちなみにこれはあってもなくてもToStringをしたときの表示が変わるくらいで、あまり意味があることではありません。

ただ、一応見て分かりやすいようにお作法だと思っていいでしょう。

[Flags]
public enum Magics
{
    Hyado = 1 << 0,     //2進数だと0001　(10進数だと1)
    Gira = 1 << 1,      //2進数だと0010　(10進数だと2)
    Hoimi = 1 << 2,     //2進数だと0100　(10進数だと4)
    Mera = 1 << 3       //2進数だと1000　(10進数だと8)
    }

またFlag属性を使うときはusing Systemを書くことを忘れずにしましょう。

フラグを立てる

フラグを立てるときはOR演算(A | B)を用います。

Magics magics = Magics.Gira | Magics.Mera;      //Gira, Mera

これは2進数のこのような性質を用いることで実現しています。

A	B	A｜B
0	0	0
0	1	1
1	0	1
1	1	1

f:id:hanaaaaaachiru:20191006174720p:plain

特定のフラグの操作をしたいとき

加えて特定のフラグの操作をしたいときはこのように書きます。

Magics magics = Magics.Gira | Magics.Mera;      //Gira, Mera
magics |= Magics.Hoimi;                         //Gira, Hoimi, Mera
magics &= ~Magics.Hoimi;                        //Gira, Mera

フラグをFalseにするのは少しだけややこしく、AND演算(A & B)とNOT演算(~A)を用います。

A	B	A & B
0	0	0
0	1	0
1	0	0
1	1	1

A	~A
0	1
1	0

f:id:hanaaaaaachiru:20191006175942p:plain

フラグの判定をする

フラグの判定はAND演算(A & B)を用いて行います。

Magics magics = Magics.Gira | Magics.Mera;      //Gira, Mera

if((magics & Magics.Mera) == Magics.Mera)
{
    //True
}

if((magics & Magics.Hyado) == Magics.Hyado)
{
    //Flase
}

f:id:hanaaaaaachiru:20191006181126p:plain