二分探索木
二分探索木は「左の子の値 ≤ 親の値 ≤ 右の子の値」という制約を持つ二分木のことを指します。
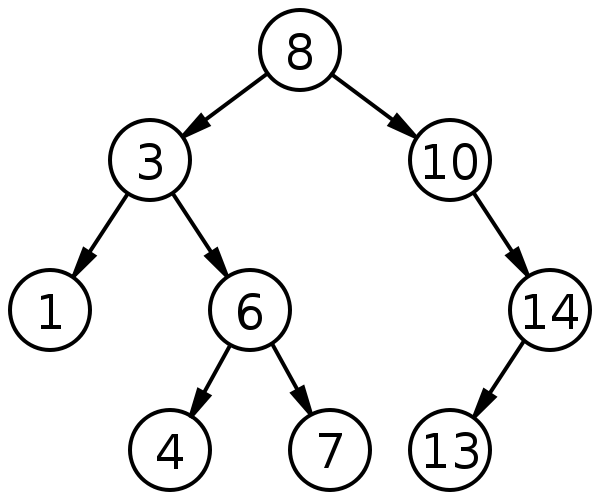
今回は以下の4つを実装します。
- 挿入
- 削除
- 要素を見つける
- 昇順で全ての要素を列挙する
コード
public class BinaryTree<T> where T : IComparable<T> { private Node _root; public BinaryTree() => _root = null; public BinaryTree(IEnumerable<T> items) { foreach (var item in items) Insert(item); } /// <summary> /// 挿入 /// </summary> /// <param name="value">挿入する値</param> public void Insert(T value) { if (_root == null) { _root = new Node(value, null); return; } Node node = _root; while (true) { if (node.Value.CompareTo(value) > 0) { if (node.Left == null) { node.Left = new Node(value, node); return; } node = node.Left; } else { if (node.Right == null) { node.Right = new Node(value, node); return; } node = node.Right; } } } /// <summary> /// 削除 /// </summary> /// <param name="value">削除する値</param> /// <returns>削除できたかどうか</returns> public bool Delete(T value) { var node = FindNode(value); if (node == null) return false; if (node.Left == null && node.Right == null) { // 子がなければ(葉である)そのまま削除 var parent = node.Parent; if (parent.Left == node) parent.Left = null; else parent.Right = null; } else if (node.Left != null && node.Right != null) { // 子が2つあるとき、左の部分木の最大値を入れ替え,削除対象ノードを削除(削除対象ノードに右の子は性質上ない) var maxNode = node.Left.Max; node.Value = maxNode.Value; var parent = maxNode.Parent; if (maxNode.Left == null) parent.Left = null; else parent.Left = maxNode.Left; } else { // 子が一つしかなければ、削除して子と置き換える var parent = node.Parent; var child = (node.Left != null) ? node.Left : node.Right; if (parent.Left == node) parent.Left = child; else parent.Right = child; } return true; } /// <summary> /// 値が存在するか探索する /// </summary> /// <param name="value">探索する値</param> public bool Find(T value) { var node = FindNode(value); if (node != null) return true; else return false; } private Node FindNode(T value) { Node node = _root; while (node != null) { if (node.Value.CompareTo(value) > 0) node = node.Left; else if (node.Value.CompareTo(value) < 0) node = node.Right; else return node; } return null; } /// <summary> /// 2分探索木を昇順で取得する /// </summary> /// <returns></returns> public IEnumerable<T> GetSortedTree() => GetSortedTree(_root); private IEnumerable<T> GetSortedTree(Node node) { if (node == null) yield break; // 中順で出力 var leftSubTree = GetSortedTree(node.Left); foreach (var element in leftSubTree) yield return element; yield return node.Value; var rightSubTree = GetSortedTree(node.Right); foreach (var element in rightSubTree) yield return element; } public class Node { public T Value { get; set; } public Node Parent { get; } public Node Left { get; set; } public Node Right { get; set; } public Node(T value, Node parent) { Value = value; Parent = parent; } /// <summary> /// このノード以下の部分木中で最大の要素 /// </summary> public Node Max { get { Node node = this; while (node.Right != null) node = node.Right; return node; } } } }
使い方
使う時はこんな感じ。
static void Main(string[] args) { var nums = new int[] { 12, 523, 22, 5, 6, 31 }; var tree = new BinaryTree<int>(nums); Console.WriteLine(tree.Find(5)); // true Console.WriteLine(tree.Find(52)); // false // 5, 6, 12, 22, 31, 523 foreach (var item in tree.GetSortedTree()) Console.WriteLine(item); Console.WriteLine(tree.Delete(15)); // false Console.WriteLine(tree.Delete(31)); // true tree.Insert(12); // 5, 6, 12, 12, 22, 523 foreach (var item in tree.GetSortedTree()) Console.WriteLine(item); }
さいごに
今回実装した二分探索木はシンプルなもので、深さが偏ってしまう可能性があります。
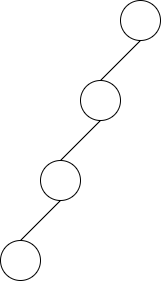
こうなってしまうと探索に時間がかかってしまう()ので、これを改善する,つまりすべての葉について深さがほぼ等しい木にするための色々な手法が考えられています。
もしかしたら平衡木といわれるものもまた記事に取り上げさせていただくかもしれません。
よかったらそちらもチェックしてみてください。
ではまた。